А вот я решила начать с первого, самого длинного модуля, опять применяю метод исключения, он часто бывает самым коротким.
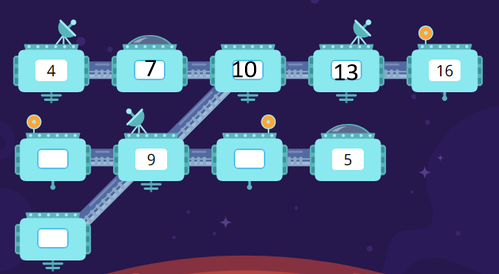
1) Первый модуль (верхний).
Допустим в каждом модуле на единицу больше космонавтов:
4 — 5 — 6 — 7 — 16 — не подходит.
Допустим в каждом модуле на два больше космонавтов:
4 — 6 — 8 — 10 — 16 — не подходит.
Допустим в каждом модуле на три больше космонавтов:
4 — 7 — 10 — 13 — 16 — Ура! Подошло!
2) Второй модуль (средний).
Здесь нужно слева увеличивать, а справа уменьшать. Допустим, что к в каждом модуле на 1 больше или меньше:
10 — 9 — 8 — 5 — не подходит.
Допустим, что к в каждом модуле на 2 больше или меньше космонавтов:
11 — 9 — 7 — 5 — Ура! Подошло!

3) Третий модуль (диагональный).
Здесь нужно найти всего одну цифру — очевидно, что это восьмерка:
10 — 9 — 8.
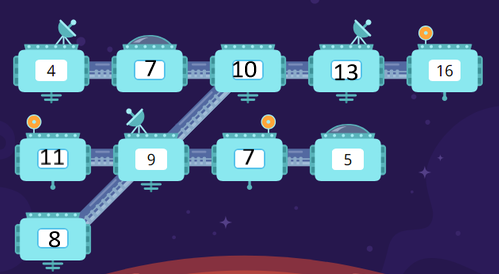
Это задание не на много сложнее, чем задание для первого класса. Здесь также нужно найти космонавтов для свободных модулей. И здесь также три линии.
Начнём с линии по середине, там модулей всего четыре из которых известно уже два числа.
Воспользуемся следующим методом для подсчёта.
Предположим, что нам нужно сначала найти число, которое находится между 9 и 5, это может быть лишь одно число 7, которое мы увеличили на 2.
Значит, 5+2=7; 7+2=9 => к 9 нужно прибавить 2, чтобы получилось желаемое число. 9+2=11
Теперь нам нужно посчитать верхнюю линию, и только затем третью линию.
Нам здесь также известно два числа 4 и 16, нужно найти сколько космонавтов в трёх других модулях. Если бы там было 4 модуля, то можно было бы предположить, что искомое число 4, 4+4=8; 8+4=12; 12+4=16,
Но у нас есть ещё один модуль, а если мы из трёх модулей заберём по одному космонавту и добавим в каждый из них не по 4, а по 3 космонавта, давайте посчитаем что получится:
4+3=7; 7+3=10; 10+3=13; 13+3=16 мы добились желаемого результата, значит данное решение нам подходит.

Остаётся последняя линия из трёх модулей из которых известно два значения. Это самое лёгкое решение на мой взгляд, т.к нам известно число 10 и 9, 10-1=9
9-1=8, таким образом нам нужно отнять лишь одного космонавта.

Вначале займемся средней линией. Известно количество космонавтов в двух модулях-5 и 9
Для выполнения условия задача о том, что количество космонавтов на линии в каждом следующем модуле отличается от предыдущего на одно и то же число,
получаем справа налево :5,7,9,11
В верхней линии тоже известно количество космонавтов в двух крайних модулях. Это 4 и 16. Модули разделяют 3 ячейки .
Для того что бы выполнилось условие задачи, в качестве разницы подхолит число 3.
Получаем слева направо 4,7,10,13,16
4+3=7
7+3=10
10+3=13
13+3=16
Остался модуль из трех ячеек.
Количество космонавтов в двух соседних известно. Это 10 и 9
Ищем разницу
10-9=1
Находим количество космонавтов в третьем модуле
9-1=8
Линия состоит из модулей, в которых живут сверху вниз 10,9,8 космонавтов.












